Question

For the following equations are there no solutions, one solution or many solutions? First: -x-4y-z=7 next -3x+4y+5z=-3 and then x+2y=-4.

Answer 1

First let's solve the third equation x+2y= -4 for "x":

`\begin{gathered} x+2y=-4 \\ x=-4-2y \end{gathered}`

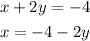
Now we substitute this into the first equation and solve for "z":

`\begin{gathered} -x-4y-z=7 \\ -\left(-4-2y\right)-4y-z=7 \\ 4+2y-4y-z=7 \\ 4-2y-z=7 \\ 4-2y-7=z \\ -3-2y=z \end{gathered}`

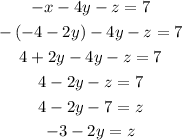
Next we substitute the "x" found in the first part and the "z" calculated latter into the second equation:

`\begin{gathered} -3x+4y+5z=-3 \\ -3(-4-2y)+4y+5(-3-2y)=-3 \\ 12+6y+4y-15-10y=-3 \\ -3+0y=-3 \\ -3=-3 \end{gathered}`

Finally, because substituting all equations we got something in the form 1=1, it means that there is infinite solutions.