Question

How would you graph f(x)=3x-1

Answer 1

If you want to graph a linear function, you only need to identify two points: the intercept on the x-axis, and the intercept on the y-axis.

The intercept on the x-axis is defined as the value of x that makes y = 0. In this case, the value is 1/3 because:

`\begin{gathered} y=3x-1\text{ \lparen We first make y=0\rparen} \\ 0=3x-1\text{ \lparen Then we find the value of x\rparen} \\ x=(1)/(3) \end{gathered}`

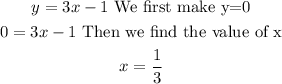
Therefore the first point is (1/3, 0)

The intercept on the y-axis is defined as the value of y that makes x = 0. In this case, the value is -1 because:

`\begin{gathered} y=3x-1\text{ \lparen We make x=0\rparen} \\ y=3(0)-1\text{ \lparen We find the value of y\rparen} \\ y=-1 \end{gathered}`

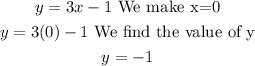
Therefore, the second point is (0,-1)

Finally, we know that between two points there is only on line that connects them (and it is the original function). So we graph these two points and connect them with a straight line:

And that is how you graph a linear function!

Is (3,1) part of the function?

Remember that we see a point (coordinate) belongs to a function if x is on its domain and y is the image of that value of x. In this case, we want to know what is the image of x = 3, to find it we replace that value in the function:

`\begin{gathered} y=3(x)-1 \\ y=3(3)-1 \\ y=9-1=8 \end{gathered}`

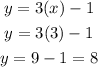
Therefore, if x is equal to 3 then y is equal to 8. In conclusion, (3,1) does not belong to the function.

What is the meaning of the number that accompanies the x?

That value is the slope of the function. It describes how the rate change of y when x varies one unit. In this case, the slope is 3.

What is the meaning of the constant number?

The constant number is the intercept on the y-axis.