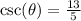a point on the terminal side of angle theta is given. Find the exact value of each of the six trigonometric functions of theta.
given point- (-12, 5)
see the attached figure to better understand the problem
we have that
the point P lies on the II quadrant
that means
the function cosine is negative
the function sine is positive
the function tangent and cotangent are negative
the function secant is negative and the function cosecant is positive
step 1
cos(x)
Applying the Pythagorean Theorem find out the hypotenuse of the right triangle
c^2=12^2+5^2
c^2=144+25
c^2=169
c=13
cos(x)=12/13
Remember that the cosine of angle theta is negative
therefore
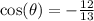
step 2
Find out sin(x)
sin(x)=5/13
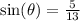
step 3
Find out tan(x)
tan(x)=5/12
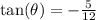
step 4
cot(x)
cot(x)=12/5

step 5
sec(x)
sec(x)=1/cos(x)
sec(x)=13/12
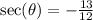
step 6
csc(x)
csc(x)=1/sin(x)
csc(x)=13/5