Question

Part 2 is vertex , axis of symmetry and x intercept

Answer 1

`h(x)=x^2-2x+1`

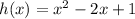
Quadratic equation in standard form:

`\begin{gathered} f(x)=ax^2+bx+x \\ \\ \end{gathered}`

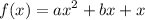
The given equation is written in standard form

Vertex:

To find the vertex first you need to find the axis of symmetry (x-value on the vertex):

`\begin{gathered} f(x)=ax^2+bx+c \\ \\ \text{axis of symmetry:} \\ x=-(b)/(2a) \\ \\ \\ \\ x=-((-2))/(2(1))=(2)/(2)=1 \end{gathered}`

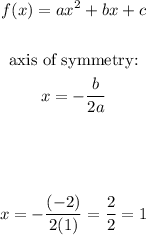
Axis of symmetry: x=1

Then, find the value of the function in x=1

`\begin{gathered} h(1)=1^2-2(1)+1 \\ h(1)=1-2+1 \\ h(1)=0 \end{gathered}`

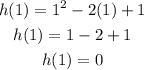
Vertex: (1,0)

x-intercept: point where the graph cross the x-axis (when h(x) is 0)

the x-intercept of the given function is the vertex, because h(x)=0 in (1,0)

x-intercept: (1,0)