In order to find the distance from the image to the lens, we can use the formula below:
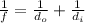
Where f is the focal length (in m), do is the object distance and di is the image distance.
So, using f = 0.3 m and do = 4di, we have:
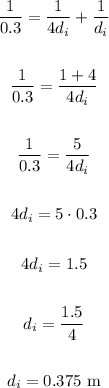
Therefore the distance from the image to the lens is 37.5 cm.