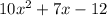
To factor this polynomials, we will use the method "slide and divide".
First, we will multiply the first numerical coefficient 10 to the last term 12, so the expression becomes:
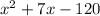
Our next step here is to find factors of the last term -120 that when added, the result is the middle term 7.
The possible factors of -120 are:
-1 and 120
1 and -120
2 and -60
-2 and 60
3 and -40
-3 and 40
4 and -30
-4 and 30
5 and -24
-5 and 24
6 and -20
-6 and 20
8 and -15
-8 and 15
10 and -12
-10 and 12
After determining all the possible factors of -120, let's add the pairs and see which pair would give us the middle term +7.
-1 and 120 = 119
1 and -120 = -119
2 and -60 = -58
-2 and 60 = 58
3 and -40 = -37
-3 and 40 = 37
4 and -30 = -26
-4 and 30 = 26
5 and -24 = 19
-5 and 24 = 19
6 and -20 = -14
-6 and 20 = 14
8 and -15 = -7
-8 and 15 = 7
10 and -12 = -2
-10 and 12 = 2
As we can see above, the factors of -120 that gives us +7 is -8 and 15. Hence, the possible factors of x² + 7x - 120 are:
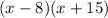
Remember that we multiplied the first term 10 to the last term -12. Our next step here is to divide -8 and +15 with 10 and simplify if needed.
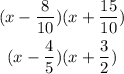
Since the coefficient is a fraction, let's simplify it further.
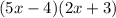
Hence, the factors of 10x² + 7x - 12 are (5x - 4) and (2x + 3).