STEP 1: Find the z scores of 91
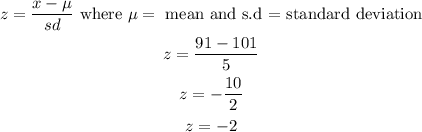
STEP 2
To find the probability that a value selected at random is in the following interval of at least 91.
We get the probability that a value selected at random is in the following interval of at most 91, and subtract it from 1.
Pr(at least 91)= 1 - Pr(at most 91)
Pr(at least 91)= 1 - probabilites less than a z - score of -2 from the graph
Pr(at least 91) = 1-(0.017+0.005+0.001)
=0.977
Therefore the probability of at least 91 =0.977
That is 97.7%