Question

Find the surface area, volume & diagonal of cuboid if the length breadth & height are 4cm, 3cm & 12cm respectively.

Answer 1

Given:

The dimensions of the cuboid are:

length (l) = 4cm

breadth (b) = 3cm

height (h) = 12cm

The volume of the cuboid

The volume (V) of a cuboid can be found using the formula:

`\begin{gathered} V\text{ = l}* b* h \\ \end{gathered}`

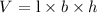
Substituting we have:

`\begin{gathered} V\text{ = 4 }*\text{ 3 }*\text{ 12} \\ =\text{ 144 cubic centimeters} \end{gathered}`

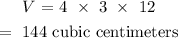
The surface area (SA) of the cuboid:

The surface area of a cuboid can be calculated using the formula:

`SA\text{ = }2lb\text{ + 2lh + 2bh}`

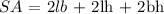
Substituting we have:

`\begin{gathered} SA\text{ = 2 }*4*3\text{ + 2}*4*12\text{ + 2}*3*12 \\ =\text{ 192 square centimeters} \end{gathered}`

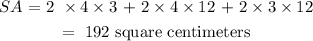
The diagonal length of cuboid:

The diagonal (d) of a cuboid can be found using the formula:

`d\text{ = }\sqrt[]{l^2^{}+b^2+h^2}`

Substituting we have:

`\begin{gathered} d\text{ = }\sqrt[]{4^2+3^2+12^2} \\ =\text{ 13 cm} \end{gathered}`

Answer summary

Volume = 144 cubic centimeters

Surface area = 192 square centimeters

length of diagonal = 13cm