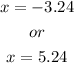Question

What are the solutions of x^2-2x-17=0

Answer 1

The solutions to the equation are:

`\begin{gathered} x=-3.24 \\ or \\ x=5.24 \end{gathered}`

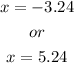
Step-by-step explanation:

Given the equation below;

`x^2-2x-17=0`

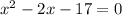
We want to find the solutions of the quadratic equation.

Applying the quadratic formula;

`x=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a}`

from the given equation;

`\begin{gathered} a=1 \\ b=-2 \\ c=-17 \end{gathered}`

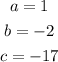
substituting the values;

`\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(1)(-17)}}{2(1)} \\ x=\frac{2\pm\sqrt[]{4^{}+68}}{2} \\ x=\frac{2\pm\sqrt[]{72}}{2} \\ x=\frac{2\pm2\sqrt[]{18}}{2} \\ x=1\pm\sqrt[]{18} \\ \\ x=1-\sqrt[]{18} \\ x=-3.24 \\ or \\ x=1+\sqrt[]{18} \\ x=5.24 \end{gathered}`

Therefore, the solutions to the equation are;

`\begin{gathered} x=-3.24 \\ or \\ x=5.24 \end{gathered}`