Question

Use the standard normal distribution or the t-distribution to construct a 90% confidenceinterval for the population mean. Justify your decision. If neither distribution can be used,explain why. Interpret the results,In a random sample of 50 people, the mean body mass index (BMI) was 26.9 and thestandard deviation was 6.06

Answer 1

(25.46, 28.34)

Explanation:

Given:

n (sample size) = 50

m (mean) = 26.9

sd (standard deviation) = 6.06

The formula for the confidence interval is:

`CI=m\pm t_(critical)\left((sd)/(√(n))\right)`

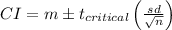
The t- critical value at the 90% confidence level with 42 degrees of freedom is: 1.682.

Therefore, we replacing:

`\begin{gathered} CI=26.9\pm1.682\cdot\left((6.06)/(√(50))\right) \\ CI=26.9+1.682\cdot\left((6.06)/(√(50))\right)=28.34 \\ CI=26.9-1.682\cdot\left((6.06)/(√(50))\right)=25.46 \end{gathered}`

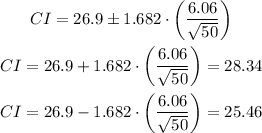
The 90% confidence interval is (25.46, 28.34)