Given that
The height of the tent is 4 feet and the length of the rope is 8 feet.
We have to find the distance of the rope from the tent.
Explanation -
The given diagram is
Here the given diagram is making a right-angled triangle.
So we will use the Pythagoras theorem to find the required length.
The Pythagoras theorem is given as
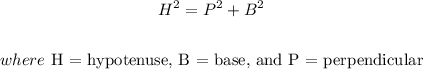
Here Hypotenuse = H = 8 feet, Base = B = ?, and Perpendicular = P = 4 feet.
Then,
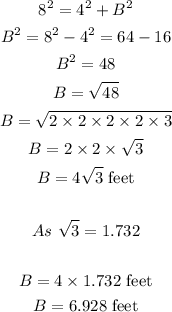
So the required distance will be 6.928 feet.
Hence, C is the correct option.
Final answer -
Therefore the final answer is 6.928