Question

when solving the system below algebraically using the substitution method, which of the following could be an equation you could create to solve for y?A. -3y + 14 = - 6y -28B. -5(-3y + 14) + 6y = - 28C. -5(3y - 14) + 6y = - 28D. -2x + 28 = 5x - 28

Answer 1

If we will start by solving for y, it means that x is substituted in one of the equations.

If we clear the value of x from the first equation and replace it in the second equation, we would get:

`\begin{gathered} x+3y=14 \\ x=-3y+14 \end{gathered}`
`\begin{gathered} -5x+6y=-28 \\ -5(-3y+14)+6y=-28 \end{gathered}`

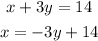
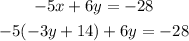
Option A does not correspond to an equation of the system as it would be:

`\begin{gathered} -3y+14=-6y-28 \\ x=-3y+14\longrightarrow x=-6y-28 \\ x+6y=-28 \end{gathered}`

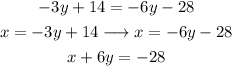
It is ignoring the coefficient -5 that multiplies x in the second equation.

Option B is exactly the result we have obtained from the substitution, so this is the equation.

Option C has the sign wrong as x=-3y+14.

Option D does not substitute x, so it won't be the step to solve for y.

Answer: Option B.