1 Answer

Verjas · Answer 1 · 2023-12-11T05:09:30+0000

Start by passing the miles into kilometers, taking into account that 1 mile is approximately 1.6km

$5mi\cdot\frac{1.6\operatorname{km}}{1mi}\cong8\operatorname{km}$

pass the kilometers to meters taking into account that 1 km is 1000m

$8\operatorname{km}\cdot\frac{1000m}{1\operatorname{km}}=8000m$

convert the 45 minutes to hours taking into account that 1 hour has 60 minutes

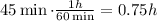
$45\min \cdot(1h)/(60\min )=0.75h$

divide the meters he ran by the time it took him to run that distance

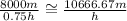
$(8000m)/(0.75h)\cong(10666.67m)/(h)$

He can run about 10666.67 m in 1 hour

another different way to find the equivalences is to write it as relations

$\begin{gathered} 1mi\Rightarrow1.6\operatorname{km} \\ 5mi\Rightarrow x \end{gathered}$
$(x)/(5mi)=\frac{1.6\operatorname{km}}{1mi}$

solve for x

$\begin{gathered} x=\frac{1.6\operatorname{km}\cdot5mi}{1mi} \\ x=8\operatorname{km} \end{gathered}$

Please log in or register to add a comment.