Question

An optometrist prescribes a corrective lens with a power of +1.5 diopters. The lens maker will start with glass blank with an index of refraction of 1.6 and a convex front surface whose radius of curvature is 20 cm. To what radius of curvature should the other surface be ground?

Answer 1

Given:

The power of the lens is,

`P=+1.5\text{ D}`

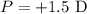
The refractive index of the lens is,

`n=1.6`

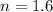
The radius of curvature of the convex surface is,

`\begin{gathered} R_1=20\text{ cm} \\ =0.20\text{ m} \end{gathered}`

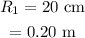
To find:

The radius of curvature of the other surface

Step-by-step explanation:

If the radius of curvature of the other surface is

`R_2`

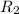
we can write,

`(1)/(f)=P=(n-1)((1)/(R_1)-(1)/(R_2))`

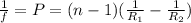
Now, substituting the values we get,

`\begin{gathered} 1.5=(1.6-1)((1)/(0.20)-(1)/(R_2)) \\ (1.5)/(0.6)=(1)/(0.20)-(1)/(R_2) \\ (1)/(R_2)=(1)/(0.20)-(1.5)/(0.6) \\ (1)/(R_2)=2.5 \\ R_2=0.40\text{ m} \\ R_2=40\text{ cm} \end{gathered}`

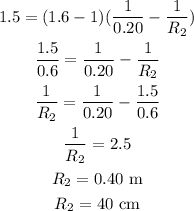
Hence, the radius of curvature of the other surface is 40 cm.