Answer:
• Vinegar: 40 milliliters
• Italian dressing: 280 milliliters
Explanation:
Let the amount of vinegar to be used = x
Let the amount of Italian dressing to be used = y
The chef wants to make 320 milliliters of the mixture.
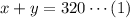
The chef plans to mix 100% vinegar with Italian dressing(12% vinegar) to make 320 milliliters of a mixture that contains 23% vinegar.
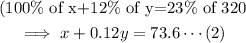
Thus, we have a system of linear equations.
![\begin{gathered} x+y=320\operatorname{\cdots}(1) \\ x+0.12y=73.6\operatorname{\cdots}(2) \end{gathered}]()
Subtract (2) from (1):
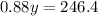
Divide both sides by 0.88
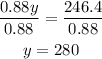
Using equation (1), we solve for x:
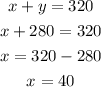
Therefore, the chef should use 40 milliliters of Vinegar and 280 milliliters of Italian dressing.