1 Answer

Hanuman · Answer 1 · 2023-04-05T10:10:15+0000

Problem:

Let's denote the above equation like this:

x-3y = -12 EQUATION 1

2x + y = 11 EQUATION 2

Solve x from equation 2:

2x = 11-y

this is equivalent to say (EQUATION 3)

$x\text{ = }(11-y)/(2)$

Now, replace the variable x in equation 1, that is:

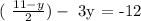
$(\text{ }(11-y)/(2))-\text{ 3y = -12}$

this is equivalent to say:

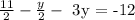
$(11)/(2)-(y)/(2)-\text{ 3y = -12}$

Putting together similar terms on different sides of the equation we get:

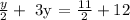
$(y)/(2)+\text{ 3y = }(11)/(2)+12$

this is equivalent to:

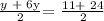
$\frac{y\text{ + 6y}}{2}\text{= }\frac{11+\text{ 24}}{2}$

this is equivalent to:

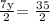
$\frac{7\text{y}}{2}\text{= }(35)/(2)$

this is equivalent to:

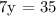
$7\text{y = 35}$

solve for y:

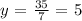
$y\text{ = }(35)/(7)\text{ = 5}$

then, we can conclude that y = 5. But, from lines back we know that x is equal to (EQUATION 3):

$x\text{ = }(11-y)/(2)$

Replacing y in the previous equation, we obtain

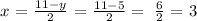
$x\text{ = }(11-y)/(2)\text{ = }(11-5)/(2)=\text{ }(6)/(2)\text{ = 3}$

then, we can conclude that:

X = 3

Y = 5

Please log in or register to add a comment.