Given,
The revenue is directly varies to the number of gallon sold.
The revenue of the gas is $51 when the number of gas sold is 15 gallons.
Required
The revenue amount when the number of gas sold is 5.5 gallons.
According to the question,

Here, R = revenue, k is proportionality constant and N = number of gallons sold.
Substituting the values then,
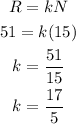
The value of k is 17/5.
The linear equation that relates R to number of gallons of gas is:
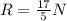
The amount of revenue at 5.5 gallons of gas sold.
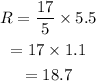
Hence, the revenue amount is $18.7.