Question

(x^3-5x^2)+(2x-10)Find all 0's

Answer 1

Given:

`\mleft(x^3-5x^2\mright)+\mleft(2x-10\mright)`

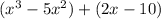
You can find all its zeros, as follows:

1. Make the expression equal to zero:

`(x^3-5x^2)+(2x-10)=0`

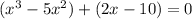
2. Distribute the positive sign. Remember the Sign Rules for Multiplication:

`\begin{gathered} +\cdot+=+ \\ -\cdot-=- \\ +\cdot-=- \\ -\cdot+=- \end{gathered}`

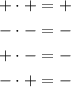
Then:

`x^3-5x^2+2x-10=0`

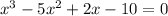
3. Factor the expression:

- Make two groups using parentheses:

`(x^3-5x^2)+(2x-10)=0`

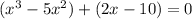
- Identify the Greatest Common Factor of each group. For the first group:

`GCF=x^2`

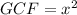
And for the second group:

`GCF=2`

- Factor them out:

`x^2(x^{}-5^{})+2(x-5)=0`

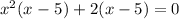
4. Notice that this expression is common in both terms:

`x-5`

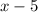
Then, you can factor it out:

`(x-5)(x^2+2)=0`

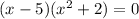
5. Now you can set up these two equations:

`\begin{gathered} x-5=0\text{ (Equation 1)} \\ \\ x^2+2=0\text{ (Equation 2)} \end{gathered}`

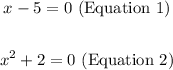
6. Solve for "x" from each equation:

- For Equation 1:

`x_1=5_{}`

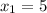
- For Equation 2:

`\begin{gathered} x^2=-2 \\ x_{}=\pm\sqrt[]{-2} \end{gathered}`

By definition:

`\sqrt[]{-1}=i`

Then, you get:

`x=\pm\sqrt[]{-2}\Rightarrow\begin{cases}x_2=i\sqrt[]{2} \\ \\ x_3=-i\sqrt[]{2}\end{cases}_{}`

Hence, the answer is:

`\begin{gathered} x_1=5_{} \\ \\ x_2=i\sqrt[]{2} \\ \\ x_3=-i\sqrt[]{2} \end{gathered}`