Question

I need help with this problem, and my app had crashed the last time I was getting an answer… So if you are the same tutor I am sorry

Answer 1

Step-by-step explanation:

Given the below function;

`f(x)=√(-2x+2)`

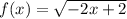
*To find f(-2), we'll go ahead and substitute x with -2 and evaluate;

`\begin{gathered} f(-2)=√(-2(-2)+2)=√(4+2)=√(6)=2.45 \\ \therefore f(-2)=2.45 \end{gathered}`

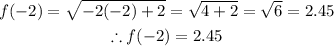
So f(-2) = 2.45

*To find f(-1), we'll go ahead and substitute x with -1 and evaluate;

`\begin{gathered} f(-1)=√(-2(-1)+2)=√(2+2)=√(4)=2 \\ \therefore f(-1)=2 \end{gathered}`

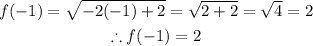
So f(-1) = 2

*To find f(0), we'll go ahead and substitute x with 0 and evaluate;

`\begin{gathered} f(0)=√(-2(0)+2)=√(0+2)=√(2)=1.41 \\ f(0)=1.41 \end{gathered}`

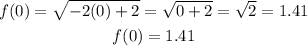
So f(0) = 1.41

*To find f(1), we'll go ahead and substitute x with 1 and evaluate;

`\begin{gathered} f(1)=√(-2(1)+2)=√(-2+2)=√(-4) \\ f(1)=NDE \end{gathered}`

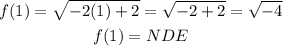
Since we have a negative root, the output doeswe'll use NDE