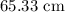Question

A cable is wrapped tightly around two pulleys whose radii are 3 and 5 ft, and whose centers are 20 ft apart. Find the length of the cable?

Answer 1

Given a cable is wrapped tightly around two pulleys whose radii are 3 and 5 ft, and whose centers are 20 ft apart. We can find the length of the cable below.

Step-by-step explanation

A diagrammatic representation of the question is given below:

The length of the belt consists of four parts: two segments tangent to the two circles, and two circular arcs.

To determine the length of the tangent segments, we draw a line from the center of the small circle perpendicular to the radius of the large circle. Since the radius of each circle is perpendicular to the tangent segment at the point of tangency, this forms a rectangle. The length of the tangent segment is equal to the length of the opposite side of the rectangle, which is a leg of a right triangle with a hypotenuse of 20 cm and another leg of length 2 cm. So the length of each tangent segment is

`Length=\sqrt[]{20^2-2^2}=\sqrt[]{400-4}=\sqrt[]{396}=\sqrt[]{36*11}=6\sqrt[]{11}`

To compute the lengths of the two circular arcs, we start by computing the angle θ in our right triangle:

`\begin{gathered} \cos \theta^{}=(2)/(20) \\ \theta=\cos ^(-1)(1)/(10) \\ \end{gathered}`

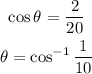
This is also the angle between the radius of the small wheel and the horizontal line joining the two centers in the diagram, and twice this angle is the central angle that subtends the circular arc on the small wheel. So the length of the part of the belt that is wrapped around the small wheel is approximately

`2\cos ^(-1)(1)/(10)*3\approx8.8238cm.`

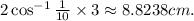
Meanwhile, the central angle that subtends the circular arc on the large wheel is

`(2\pi-2\cos ^(-1)(1)/(10))radians`

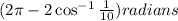
and thus the length of the part of the belt that is wrapped around the large wheel is

`\mleft(2\pi-2\cos ^(-1)(1)/(10)\mright)\cdot5\approx16.7096cm.`

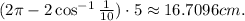
So the total length of the belt should be

`2\cdot6\sqrt[]{11}+8.8238+16.7096\approx65.33cm.`

Answer:

`65.33\text{ cm}`