Question

What is the probability of pulling out a baseball? Enter your in this order.reduced fraction decimal, and then percent

Answer 1

The bag has a total of 10 balls:

2 baseballs (B)

5 tennis balls (T)

3 whiffle balls (W)

To determine the probability of pulling out a baseball you have to divide the number of baseballs on the bag by the total number of balls:

`\begin{gathered} P(B)=\frac{nº\text{baseballs}}{\text{Total}\mathrm{}\text{balls}} \\ P(B)=(2)/(10)=0.2 \end{gathered}`

Multiply the result by 100 to express it as a percentage:

`0.2\cdot100=20\%`

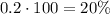
Considering that we calculated the probability based on a sample, this probability can be classified as empirical or experimental.

The experiment is "pull a ball from the bag and register its type"

There are 10 balls on the bag, which means that there are 10 possible outcomes on the sample space.

`S=\mleft\lbrace B,B,T,T,T,T,T,W,W,W\mright\rbrace`

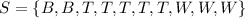
For this experiment, choosing a baseball is the favorable outcome, or success of the experiment, since it is the type of ball we intend to choose.

To determine the probability of choosing a tennis ball you have to proceed as follows.

Calculate the quotient between the number of tennis balls on the bag (favorable outcome) by the total number of balls.

`\begin{gathered} P(T)=\frac{nº\text{tennisballs}}{\text{total}\mathrm{}\text{balls}} \\ P(T)=(5)/(10)=0.5 \end{gathered}`

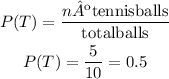
Multiply the result by 100 to express it as a percentage:

`0.5\cdot100=50\%`

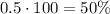
The probability of pulling a baseball is 20% while the probability of choosing a tennis ball is 50%, since the probability of choosing a tennis ball is higher, then this event is more likely.