Question

Determine whether the system is independent, inconsistent, or dependent.-x+4y=101/2x-2y=14Select one:O a. InconsistentO b. DependentOc. Independentd. None of these

Answer 1

Step-by-step explanation:

Given;

We are given the following system of equations;

`\begin{gathered} -x+4y=10---(1) \\ \\ (1)/(2)x-2y=14---(2) \end{gathered}`

Required;

We are required to determine if the system of equations is dependent, independent or inconsistent.

Step-by-step solution;

We will start by taking equation (1). From this we make x the subject of the equation;

`\begin{gathered} -x+4y=10 \\ \\ -x=10-4y \\ \\ Multiply\text{ }all\text{ }through\text{ }by\text{ }-1: \\ x=-10+4y \end{gathered}`

Next step is to substitute the value of x into equation (2);

`\begin{gathered} (1)/(2)x-2y=14 \\ \\ (1)/(2)(-10+4y)-2y=14 \end{gathered}`
`-5+2y-2y=14`

We now collect all like terms;

`\begin{gathered} 2y-2y=14+5 \\ \\ 0=19 \end{gathered}`

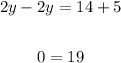
This equation is not true since zero does not equal to 19.

Therefore;

ANSWER:

The equations are INCONSISTENT.

There is no solution based on our calculations above.