The total area of a rectangular-shaped garden is:
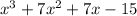
We have that the area of a rectangle is
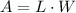
We have the total area given by the expression above. We also have the length, given by:
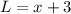
Then
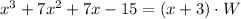
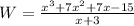
We need to solve this polynomial division:
Therefore, the width is
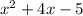
The perimeter is the sum of all the sides of the rectangle:
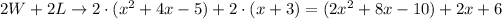
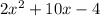
So, the perimeter is 2x^2+10x-4.
The width is x^2+4x-5.