Question

Hiw do I write the equation of a circle in SF given the center and the radius

Answer 1

We will see how to formulate the equation of the circle in its standard form.

The equation of a circle is defined by the following two parameters:

`\begin{gathered} C\colon\text{ Center cartesian coordinates ( a , b )} \\ r\colon\text{ Radius of the circle} \end{gathered}`

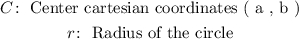
A circle is defined by its radial length ( r ) also known as the radius of a circle and the location of the circle which is defined by its center ( C ).

The standard form ( SF ) of the equation of a circle in a cartesian coordinate system is given as follows:

`(x-a)^2+(y-b)^2=r^2`

We will use the above standard form of the equation of a circle to define a circle given its Center coordinates ( C ) and radius ( r ).

a) C = ( 0 , 0 ) , r = 7

For the above parameters we will subsitute the respective quantities as follows:

`\begin{gathered} C\text{ = ( 0 , 0 ) , a = b = 0} \\ \\ (x-0)^2+(y-0)^2=7^2 \\ \textcolor{#FF7968}{x^2+y^2}\text{\textcolor{#FF7968}{ = 49}} \end{gathered}`

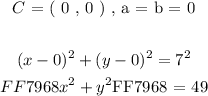
b) C = ( 2 , 3 ) , r = 6

For the above parameters we will subsitute the respective quantities as follows:

`\begin{gathered} C\text{ = ( 2 , 3 ) , a = 2 , b = 3} \\ \\ (x-2)^2+(y-3)^2=6^2 \\ \textcolor{#FF7968}{(x-2)^2+(y-3)^2=36} \end{gathered}`

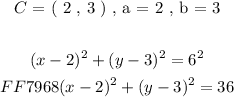
In the similar way we can express the (SF) of the equation of a circle given C and r.