Question

I need help with this problem. it’s calc 1 in high school

Answer 1

-1

Explanation:

Given the limit below:

`\lim _(x\to\infty)\mleft((9-√(x))/(3+√(x))\mright)`

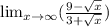
Follow the steps below to find the limit.

Step 1: Divide both the numerator and denominator by √x.

`\lim _(x\to\infty)\mleft(\frac{\frac{9-\sqrt[]{x}}{\sqrt[]{x}}}{\frac{3+\sqrt[]{x}}{\sqrt[]{x}}}\mright)=\lim _(x\to\infty)\mleft(\frac{\frac{9}{\sqrt[]{x}}-1}{\frac{3}{\sqrt[]{x}}+1}\mright)`

Step 2: Next, apply the given rule of limits below:

`\begin{gathered} \lim _(x\to\infty)\mleft((f(x))/(g(x))\mright)=(\lim_(x\to\infty)\mleft(f(x)\mright))/(\lim_(x\to\infty)\mleft(g(x)\mright)),g(x)\\eq0 \\ \implies\lim _(x\to\infty)\mleft(\frac{\frac{9}{\sqrt[]{x}}-1}{\frac{3}{\sqrt[]{x}}+1}\mright)=\frac{\lim_(x\to\infty)\mleft(\frac{9}{\sqrt[]{x}}-1\mright)}{\lim_(x\to\infty)\mleft(\frac{3}{\sqrt[]{x}}+1\mright)} \end{gathered}`

Step 3: Find the limits.

`\begin{gathered} \lim _(x\to\infty)(\frac{9}{\sqrt[]{x}}-1)=-1 \\ \lim _(x\to\infty)(\frac{3}{\sqrt[]{x}}+1)=1 \end{gathered}`

Therefore:

`\lim _(x\to\infty)(\frac{9-\sqrt[]{x}}{3+\sqrt[]{x}})=-(1)/(1)=-1`

The limit as x tends to infinity is -1.