The Solution:
Given the function money in account A as below:
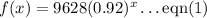
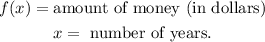
Part A:
Comparing eqn(1) with the general formula below:
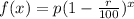
We get
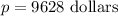
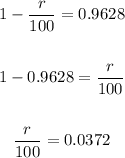
Cross multiplying, we get
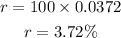
Thus, the amount of money in account A is decreasing since 0.92 is less than 1.
It is decreasing at 3.72% per year.
Part B:
Given the table below:
To compare the rate of change of the amount of money in account A and account B.
We shall find the rate of change in the amount of money in account B.
By formula,
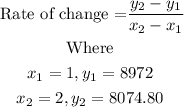
Putting these values in the formula, we get
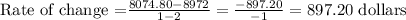
But for the money in account A, the rate of change per year is:
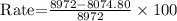
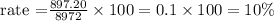
Thus, account B recorded a greater percentage change in the amount of money than account A, since the rate of account B (10%) is greater than 3.72% of account A.