Hello there. To solve this question, we'll first analyze the dimensions given for the fence and make a drawing, to lead us to the right answer.
First, let's make the drawing of the enclosured area:
We called y the length of the rectangular area and x the width.
We know that the perimeter of this rectangular area is given by:
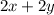
In this case, this will be equal to 280, because that's what the farmer has available to build it.
Thus, we have:
2x + 2y = 280
Divide both sides by a factor of 2
x + y = 140
Isolate the variable y, subtracting x on both sides of the equation
y = 140 - x
The area of this enclosured area is equal to x * y. Making use of the expression found on the last step, we get:
A(x) = x * (140 - x)
Apply the foil
A(x) = 140x - x²
Now, to find the maximum area, we want to find the maximum value of the quadratic function.
Remember that for a quadratic function f(x) = ax² + bx + c, for a < 0, f(x) will have a maximum value at x = -b/2a and this maximum value will be A = -(b² - 4ac)/4a.
Using the coefficients a = -1, b = 140 and c = 0, we have:
A = -(140² - 4 * (-1) * 0)/(4 * (-1))
A = -19600/(-4) = 4900 m².
This is the maximum area this enclosured region can have.