Question

The following are distances (in miles) traveled to the workplace by 23 employees of a certain hospital. 7,2, 37, 32, 27, 22, 16, 11, 6, 1, 36, 31, 25, 20, 15, 10, 5, 24, 24, 24, 9, 9, 14 Send data to calculator Draw the frequency polygon for these data using an initial class boundary of 0.5 and a class width of 9. Note that you can add or remove classes from the figure. Label each class with its midpoint. Frequency A I DO 10:0 X $ ? Soon

Answer 1

Given the following data:

`7,2,37,32,27,22,16,11,6,1,36,31,25,20,15,10,5,24,24,24,9,9,14`

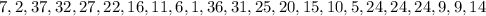
This represents the distance (in miles) traveled to the workplace by 23 employees of a certain hospital.

We need to represent this data using a frequency polygon, given that the initial class is 0.5, and a width of 9. The classes (and their midpoints) are:

`\begin{gathered} \lbrack0.5,9.5\lbrack\rightarrow5 \\ \lbrack9.5,18.5\lbrack\rightarrow14 \\ \lbrack18.5,27.5\lbrack\rightarrow23 \\ \lbrack27.5,36.5\lbrack\rightarrow32 \end{gathered}`

Now, the frequencies are:

`\begin{gathered} \text{Frequency of }\lbrack0.5,9.5\lbrack\colon7 \\ \text{Frequency of }\lbrack9.5,18.5\lbrack\colon5 \\ \text{Frequency of }\lbrack18.5,27.5\lbrack\colon7 \\ \text{Frequency of }\lbrack27.5,36.5\lbrack\colon4 \end{gathered}`

The frequency polygon is: