This is a free fall problem, a free fall problem can always be solved with one of the following equations:

For simplicity, in this case, we will assume the positive direction points down.
In this problem we want to determine the final velocity of the rock and we know:
• The displacement 111 m
,
• The acceleration due to gravity
,
• The initial velocity 0 m/s (this comes from the fact that the rock is dropped)
Given what we know and what we want to know we notice that we can use the third equation above, plugging the values we know and solving for the final velocity we have:
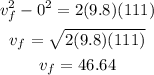
Therefore, the final velocity of the rock is 46.64 m/s.
From the equations above we notice that none of them have the mass as variable; this means that if the mass of the rock was doubled the final velocity will not change. This comes from the fact that, for all objects in the surface of Earth regarding of their masses, the acceleration due to graph is approximately 9.8 m/s²