intoTo do this, you just have to plug the value of x or y into the equation and solve to get its corresponding x or y value. So,
*If x = 2
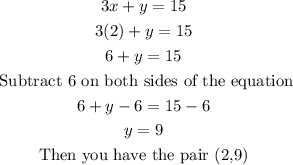
*If y = 3
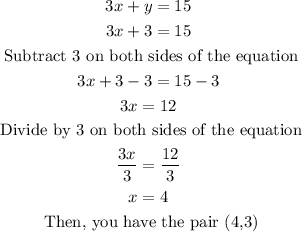
*If x = 6

*If x = 0
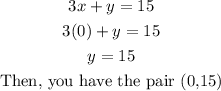
*If x = 3
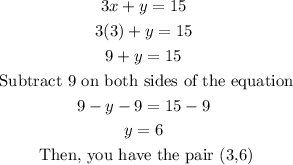
*If y = 0
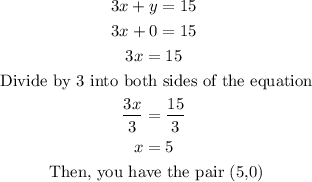
*If y = 8

Therefore, the table would be
Now, to find the slope of the line you can solve for y in the equation because that way you will have the equation of the line in its slope-intercept form, that is
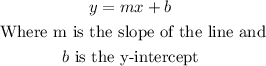
So,
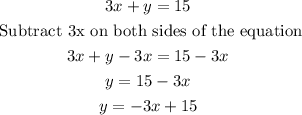
Then, in this case
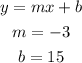
Therefore, the slope of the line is -3.