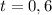Question

I only got half the answer to this question. I’m also needing the projectile return to the ground after seconds

Answer 1

We are given a function which models the height in feet of a projectile.

`s=-16t^2+v_0t`

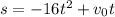
Given that the initial velocity;

`v_0=96\text{ ft per second}`

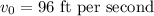
We can determine what time the projectile would return to the ground by finding the value of the equation when;

`s=0`

This is because, the heigh at the ground is zero foot.

Hence we would have the function as;

`-16t^2+96t=0`

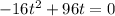
We begin by factoring both sides;

`\begin{gathered} -16t^2+96t=0 \\ 16t(-t+6)=0 \end{gathered}`

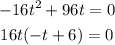
Refine the parenthesis and re-write as;

`16t(6-t)=0`

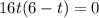
We shall now apply the rule which states;

`\begin{gathered} \text{If;} \\ ab=0 \\ \text{Then;} \\ a=0,b=0 \end{gathered}`

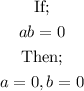
Therefore, we would have;

`\begin{gathered} 16t(6-t)=0 \\ 16t=0 \\ t=(0)/(16) \\ t=0 \\ \text{Also;} \\ 6-t=0 \\ 6=t \end{gathered}`

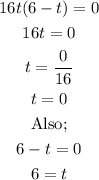
This shows that the projectile would reach the ground after 6 seconds. The other result t = 0 shows that the projectile was on the the ground at 0 seconds (just before take-off).

ANSWER:

`t=0,6`