Question

A group of scientist studied the effect of chemical on various strains of bacteria. strain A started with 12,000 cells and decreased at a constant rate of 3000 cells per hour after the chemical was applied. strain B started with 4000 cells and decreased at a constant rate of 2000 cells per hour after the chemical was applied. When will the strain have the same number of cells?

Answer 1

Since strain A started with 12,000 cells and decreased at a constant rate of 3000 cells per hour, we get that the cell population of strain A after t hours is:

`12000-3000t\text{.}`

Since strain B started with 4000 cells and decreased at a constant rate of 2000 cells per hour, we get that the cell population of strain B after t hours is:

`4000-2000t\text{.}`

If strain A and strain B have the same number of cells, then we can set the following equation:

`12000-3000t=4000-2000t\text{.}`

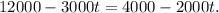
Subtracting 4000 from the above equation we get:

`8000-3000t=-2000t\text{.}`

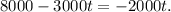
Adding 3000t to the above equation we get:

`8000=1000t\text{.}`

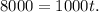
Dividing by 1000 we get:

`t=8.`

Now, notice that, substituting t=8 in the first expression in the answering tab we get:

`12000-8\cdot3000=12000-24000=-12000.`

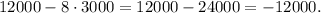
But we cannot get a negative number of cells, therefore this solution has no real meaning in the context of the problem.

Now, notice that substituting t=2 in the second expression we get:

`4000-2000\cdot2=4000-4000=0.`

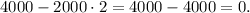
Therefore after 2 hours, strain A has 0 cells, and this number does not change with time (because we cannot get a negative number of cells).

Now, notice that substituting t=4 in the expression we get that:

`12000-3000\cdot4=12000-12000=0.`

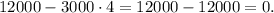
Therefore after 4 hours, strain B has 0 cells.

Then, after 4 hours after the chemical was applied both strains will have 0 cells.

Answer: 4 hours after the chemical was applied.