Need to solve for x by completing the sq and round to nearest 10th

Question

asked Nov 20, 2023 68.9k views

1 Answer

Danjuggler · Answer 1 · 2023-11-25T03:02:14+0000

Question:

Solution:

Consider the following expression:

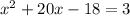
this is equivalent to:

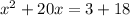
this is equivalent to:

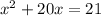
Completing the square we get:

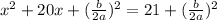
here

a= 1

b = 20

then, we obtain:

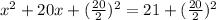
this is equivalent to:

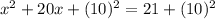
that is:

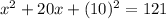
notice that the left side of the equation is a perfect square, and therefore the equation becomes:

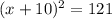
Now, to solve for x, we apply the square root to both sides of the equation and we get:

$x+10^{}=\pm\sqrt[]{121}$

solving for x, we get:

$x^{}=\pm\sqrt[]{121}-10=\pm11-10$

then, the correct answers are:

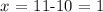
$x\text{ = 11-10 = 1}$

and

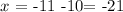
$x\text{ = -11 -10= -21}$

So that, the correct answer is:

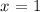
$x\text{ = 1}$

and

$x\text{ = -21}$