Question

Fernando wants to find the height of an oak tree in his yard. If Fernando stands85 ft away from the tree, and looks up at an angle of elevation of 36 degrees tothe top of the tree, and his eye line is 6 ft from the ground, then how tall is thetree? Round your answer to the nearest foot.

Answer 1

The height of the tree is : 6 + x

Using the trigonometric function : TANGENT to calculate for x

`\tan \theta=\frac{opposite\text{ }}{\text{adjacent}}`

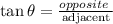
From the 36 degree angle, the opposite side is x and the adjacent side is 85

`\begin{gathered} \tan \theta=(x)/(85) \\ x=85\tan \theta \\ x=85\tan 36 \\ x=61.756ft\text{.} \end{gathered}`

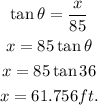
The height of the tree is 6 + x = 6 + 61.756 = 67.756 ~ 68 ft

Answer : The height of the tree is 68 ft.