Question

What is the accumulated value of periodic deposits of $40 at the beginning of every six months for 18 years if the interest rate is 4.62% compounded semi-annually?_________________Round to the nearest cent

Answer 1

We are asked to determine the future value for an annuity that is paid at the beginning of every six months with an interest rate of 4.62% compounded semi-annually (every six months). To do that we will use the following formula:

`FV_{\text{due}}=PMT(((1+i)^n-1)/(i))(1+i)`

Where:

`\begin{gathered} \text{PMT}=\text{payments in each time period} \\ i=\text{ interest rate in decimal form} \\ n=\text{ time periods} \end{gathered}`

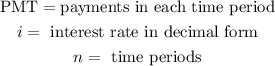
The PMT is the $40 payments every six months and the interest rate "i" in decimal form is:

`i=(4.62)/(100)=0.0462`

And the time period "n" is the number of six months in a year, since every year there are two periods of six months, in 18 years we have:

`n=18\text{years}(2periods)/(1year)=36periods`

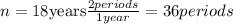
Replacing the values we get:

`FV_{\text{due}}=(40)(((1+0.0462)^(36)-1)/(0.0462))(1+0.0462)`

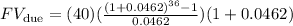
Now we solve the operations:

`FV_{\text{due}}=(40)((5.08-1)/(0.0462))(1.0462)`

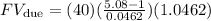
Solving the operations we get:

`FV_{\text{due}}=5168.41`

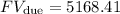
Therefore, the accumulated value is $5168.41