Solution
- The question would like us to solve the following:
![8<p>- The solution is given below:</p>[tex]\begin{gathered} 88 \\ \\ \text{ Expand the bracket} \\ \\ 9x-x^2>8 \\ \\ \text{ Rewrite the inequality, we have:} \\ -x^2+9x-8>0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/b0rcjhhsue53vz2p8oxmv3yakfiaeptsot.png)
- Now, we can factorize the expression as follows:
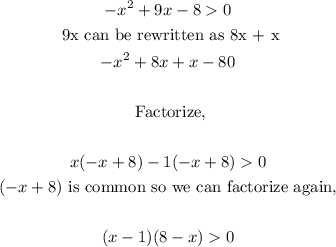
- Now, we need to decide where the solution region of the inequality is. The possible solution regions are
[tex]\begin{gathered} \text{ Region 1: }x\lt1 \\ \text{ Region 2: }1\lt x\lt8 \\ \text{ Region 3: }x>8 \\ \\ \text{ We simply need to choose the values that fall into any of these regions and test them in the } \\ \text{ original inequality for which ones are correct.} \\ \\ \text{ Region 1:} \\ \text{ Choosing }x=0,\text{ since, }x<1 \\ 88 \\ 8
- Thus, the solution to the inequality is:
[tex]1
Final Answer
The solution to the inequality is:
[tex]1