Question

3: Factor the function to determine its behavior at the x-axis.

Answer 1

D. tangent at x = 0 and and crosses at x = 3

Step-by-step explanation

Given that:

`f(x)=x^5-27x^2`

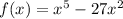
What to find:

To factor the given function and determine its behavior at the x-axis.

Step-by-step solution:

Solve for x, set f(x) equal to zero

`\begin{gathered} x^5-27x^2=0 \\ \\ x^5=27x^2 \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }x^2 \\ \\ (x^5)/(x^2)=(27x^2)/(x^2) \\ \\ x^3=27 \\ \\ Take\text{ }cube\text{ }root\text{ }of\text{ }both\text{ }sides \\ \\ \sqrt[3]{x^3}=\sqrt[3]{27} \\ \\ x=3 \end{gathered}`

From f(x) = 0, therefore, x = 0

Also using a graphical method, we have:

Hence, the behavior of the x-axis is tangent at x = 0 and and crosses at x = 3.

The correct answer is option D. tangent at x = 0 and and crosses at x = 3