Question

Rewrite in simplest radical form √x• 4√x. Show each step of your process.

Answer 1

`√(x)*\sqrt[4]{x}`

1. Find the Lowerst common multiple (LCM) of the indice:

Multiples of 2: 2,4,6,8,...

Multiples of 4: 4,8,12,16,..

LCM: 4

2. Find the number you need to multiply each original indice to get the LCM

`\begin{gathered} 2*2=4 \\ \\ 4*1=4 \end{gathered}`

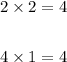
First indice needs to be multiplied by 2

Second indice needs to be multiplied by 1

3. Rewrite the expression with indice LCM and expoenent of the number inside the radical multiplied by the reults in step 2:

`√(x)*\sqrt[4]{x}=\sqrt[4]{x^2}*\sqrt[4]{x}`

4. Multiply:

`=\sqrt[4]{x^2*x}=\sqrt[4]{x^3}`Then, the simplest radical form of the given expression is:
`\sqrt[4]{x^3}`