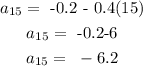Question

For the following arithmetic sequences find the explicit formula and the value of the indicated term

Answer 1

Answer:
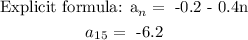
`\begin{gathered} \text{Explicit formula: a}_n=\text{ -0.2 - 0.4n} \\ a_(15)=\text{ -6.2} \end{gathered}`Explanations:

This is an Arithmetic Progression.

The common difference is calculated as follows:

`\begin{gathered} d=T_2-T_1 \\ d\text{ = -1.0 - (-0.6)} \\ d\text{ = -1.0+0.6} \\ d\text{ = -0.4} \end{gathered}`

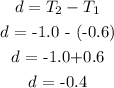
The first term, a = -0.6

The explicit formula can be calculated using the formula for the nth term of an Arithmetic Progression.

`\begin{gathered} a_n_{}=\text{ a + (n-1)d} \\ a_n=\text{ -0.6 + (n-1)(-0.4)} \\ a_n=-0.6\text{ -0.4n + 0.4} \\ a_n=\text{ -0.6 + 0.4 -0.4n} \\ a_n=\text{ -0.2 -0.4n} \end{gathered}`

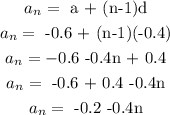
The explicit formula is therefore:

`a_n=\text{ -0.2 - 0.4n}`

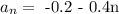
To get the value of a15, substitute n = 15 into the explicit formula gotten above

`\begin{gathered} a_(15)=\text{ -0.2 - 0.4(15)} \\ a_(15)=\text{ -0.2-}6 \\ a_(15)=\text{ }-6.2 \end{gathered}`