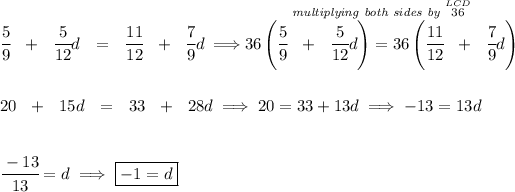we can look at this this way hmmmm let's get the LCD of all denominators and multiply both sides by it, thus doing away with the denominators.
hmmm let's see, we have denominators of 12 and 9 really, let's do a quick prime factoring on each.
9 = 3 * 3 * 1
12 = 2 * 2 * 3 * 1
well, number 3 is repeated on both so we'll add it only once, the rest we use as well, that gives us an LCD of
3 * 3 * 2 * 2 * 1 = 36
notice, the common 3 to 12 and 9, was only used once in the LCD, the others come along. hmmm so anyhow, we have an LCD of 36, let's multiply both sides by it.