the vertical asymptote and horizontal asymptote
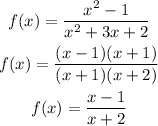
The vertical asymptote is x+2 = 0, x = -2
The horizontal asymptote is x - 1 = 0, x = 1
the x-intercept and the y-intercept
The intercept with x is calculated as 0 f(x)
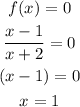
The intercept with x is (1,0)
The intercept with y is calculated for x = 0

The intercept with y is (0,-1/2)