Question

The heating element of a coffee maker operates at 120 V and carries a current of 3.50 A. How long does it take to heat 1.50 kg of water from room temperature 23oC to the boiling point? Assume that no energy is lost in the process. ( cwater = 4186 J/(kgoC))Group of answer choices12.4 minutes19.2 minutes23.6 minutes29.1 minutes

Answer 1

your answer would be 19.2 minutes!

Answer 2

19.2 minutes

Step-by-step explanation

Given:

• The voltage at which the coffee maker operates, V = 120 V

,

• The current the coffee maker carries, I = 3.50 A

,

• The mass of water to heat, m = 1.50 kg

,

• The specific heat capacity of water, c = 4186 J/kg°C

,

• The initial temperature of the water, T₀ = 23°C

,

• The final temperature of the water, T = 100°C (boiling point)

Unknown:

• The time it will take to heat the water, t, in minutes.

First, we have to find how much work has to be done to the water to raise its temperature to the boiling point,

`Q=m\cdot c\cdot\Delta T`

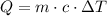
This is,

`Q=m\cdot c\cdot(T-T_o)_{}`

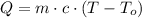
Replace with the given values and solve,

`Q=1.50kg\cdot4186(J)/(kg\cdot\degree C)\cdot(100-23)\degree C=483483J`

This work will be done by the coffee maker, which has a power of,

`P=V\cdot I=120V\cdot3.50A=420W`

Power is the rate of work per second,

`P=(W)/(t)`

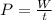
In this case, the work is Q,

`P=(Q)/(t)`

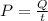
Solving for t,

`t=(Q)/(P)`

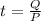
Replace with the known values,

`t=(483483J)/(420W)=1151.15s`

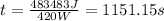
The time it will take to heat the water is 1151.15 seconds. But we have to find the time in minutes. Knowing that 1 minute is equivalent to 60 seconds, convert the time,

`t=1151.15s\cdot(1\min)/(60s)\approx19.2\min`

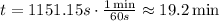
Hence, it will take 19.2 minutes for the coffee maker to heat the water from 23°C to the boiling point.