Question

How would I solve the problem in the screenshot? Thanks

Answer 1

The function is given as,

`f(x,y)=7x^2+2y^2-7x+16y-13`

Obtain partial derivative with respect to 'x' as,

`\begin{gathered} (\partial f)/(\partial x)=(\partial)/(\partial x)(7x^2+2y^2-7x+16y-13) \\ (\partial f)/(\partial x)=(14x+0-7+0-0) \\ (\partial f)/(\partial x)=14x-7 \end{gathered}`

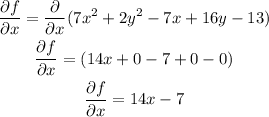
Obtain partial derivative with respect to 'y' as,

`\begin{gathered} (\partial f)/(\partial y)=(\partial)/(\partial y)(7x^2+2y^2-7x+16y-13) \\ (\partial f)/(\partial y)=(0+4y-0+16-0) \\ (\partial f)/(\partial y)=4y+16 \end{gathered}`

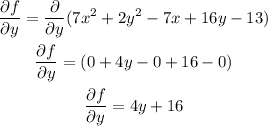
The critical points can be obtained by equating the partial derivatives to zero,

`\begin{gathered} (\partial f)/(\partial x)=0\Rightarrow14x-7=0\Rightarrow x=0.5 \\ (\partial f)/(\partial y)=0\Rightarrow4y+16=0\Rightarrow y=-4 \end{gathered}`

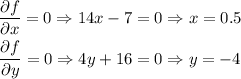
So the critical point of the function is (0.5,-4).

Obtain the second-order derivatives as,

`\begin{gathered} r=(\partial^2f)/(\partial x^2)=(\partial)/(\partial x)(14x-7)=14-0=14 \\ s=\frac{\partial^2f}{\partial x\partial y^{}}=(\partial)/(\partial x)(4y+16)=0+0=0 \\ t=(\partial^2f)/(\partial y^2)=(\partial)/(\partial y)(4y+16)=4+0=4 \end{gathered}`

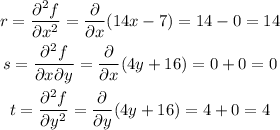
Consider the following criteria,

1. Relative Maximum:

`rt-s^2>0\text{ and }r>0\Rightarrow\text{ Relative minima }`

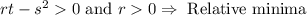
2. Relative Minimum:

`rt-s^2>0\text{ and }r<0\Rightarrow\text{ Relative maxima }`

3. Saddle Point:

`rt-s^2<0\Rightarrow\text{ Saddle Point }`

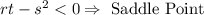
4. No Conclusion can be drawn:

`rt-s^2=0\Rightarrow\text{ Inconclusive }`

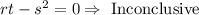
Check for the given values of second derivatives,

`\begin{gathered} r(0.5,-4)=14 \\ s(0.5,-4)=0 \\ t(0.5,-4)=4 \end{gathered}`

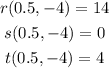
It follows that,

`\begin{gathered} rt-s^2=14(4)-(0)^2=14(4)>0 \\ r=14>0 \end{gathered}`

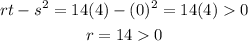
Thus, the function has a relative minimum at the critical point (0.5,-4).

The value of this maximum can be obtained by substituting the critical point coordinates in the function,

`\begin{gathered} f_(\max )=f(0.5,-4) \\ f_(\max )=7(0.5)^2+2(-4)^2-7(0.5)+16(-4)-13 \\ f_(\max )=1.75+32-3.5-64-13 \\ f_(\max )=-46.75 \end{gathered}`

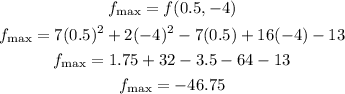
Thus, the maximum value of the function is - 46.75 which occurs at the point (0.5,-4).