Question

Previous2Next →Interpreting Expressions: Mastery TestSubmit TestΤο2Two quadratic functions are represented below.f(t) = 3 + 12х-4-3-2-101010-3-8-158X)Which sentence correctly compares the two functions?ОАThe axis of symmetry of the graph of g(x) is to the left of the axis of symmetry of the graph of Ax) because g is symmetricabout x = 1, fis symmetric about x = 3, and 1 <3.Ов,The minimum value of Rx) is greater than the maximum value of 8x) because 10) > 8(-3).OC. The value of gtx) is greater than that of Rx) at x = -2 because 8(-2) = 0, -2) = -1, and 0 > -1.OD. The axis of symmetry of the graph of g(x) is to the right of the axis of symmetry of the graph of fx because fis symmetricabout x = 0, gis symmetric about x=-3, and 0 > -3.

Answer 1

We must compare two quadratic functions.

1) First, we find the equation of the quadratic function g(x).

The general quadratic equation has the form:

`g(x)=a\cdot x^2+b\cdot x+c.`

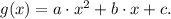
We must find the values of a, b and c. To do that, we take three points from the table:

`\begin{gathered} g(-1)=-3=a\cdot(-1)^2+b\cdot(-1)+c\Rightarrow-3=a-b+c, \\ g(0)=-8=a\cdot0^2+b\cdot0+c\Rightarrow c=-8, \\ g(1)=-15=a\cdot1^2+b\cdot1+c\Rightarrow-15=a+b+c\text{.} \end{gathered}`

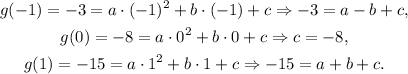
Replacing the value c = -8 in the first and second equation, we have:

`\begin{gathered} -3=a-b-8\Rightarrow a-b=5, \\ -15=a+b-8\Rightarrow a+b=-7. \end{gathered}`

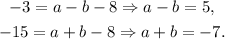
Summing the equations, we have:

`2a=5-7=-2\Rightarrow a=-1.`

Replacing the value a = -1 in one of the equations above, we get:

`b=-7-a=-7+1=-6.`

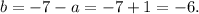
So we have the following equation for g(x):

`g(x)=-x^2-6x-8.`

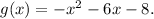
2) We plot the graph of f(x) and g(x):

A. From the graphs, we see that:

• f(x) is symmetric respect to x = 0,

,

• g(x) is symmetric respect to x = -3.

So statement A is false.

B. From the graphs, we see that:

• the minimum value of f(x) is f(0) = 3, the maximum value of g(x) is g(-3) = 1.

So statement B is true.

C. From the graphs, we see that:

• f(-2) = 7 ≠ -1,,

,

• g(-2) = 0.

We see that not all the data of statement C is true.

D. From the graphs, we see that:

• f(x) is symmetric respect to x = 0,

,

• g(x) is symmetric respect to x = -3.

So the axis of symmetry of g(x) is to the left, and statement D is false.

Answer

B. The minimum value of f(x) is greater than the maximum value of g(x) because f(0) > g(-3).