Question

What is the maximum speed at which a car can safely travel around a circular track of radius 142 meters if the coefficient of friction between the tires and the road is 1.07? Include units in your answer.

Answer 1

We have the next information

r=radius=142m

k=coeffcient of friction=1.07

The maximum frictional force is

`F=\text{kmg}`

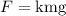
where F is the frictional force, k is the coefficient of friction, m is the mass and g is the gravity.

Also for the centripetal force we have the next formula

`F=(mv^2)/(r)`

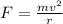
where F is the force, m is the mass , v the speed and r is the radius

we have an equivalence between the two formulas

`(mv^2)/(r)=\text{kmg}`

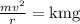
then we simplify and we isolate the speed

`v=\sqrt[]{\text{krg}}`

we substitute the values

`v=\sqrt[]{(1.07)(142)(9.8)}`

the maximum speed is

`v=38.6\text{ m/s}`

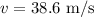
ANSWER

v=38.6 m/s