Question

Use the given value and the trigonometric identities to find the exact value of each indicated trigonometric function

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given values

`\begin{gathered} \sin 30^(\circ)=(1)/(2) \\ \tan 30^(\circ)=\frac{\sqrt[]{3}}{3} \end{gathered}`

STEP 2: Get the value of cosec 30 degrees

`\begin{gathered} \text{csc }\theta\text{ means cosec }\theta\text{ and it is the inverse of sin }\theta \\ \csc \theta=(1)/(\sin \theta) \\ \sin 30=(1)/(2) \\ \csc 30=(1)/(\sin 30) \\ By\text{ substituting 1/2 for sin 30} \\ \csc 30=(1)/((1)/(2))=1*2=2 \end{gathered}`

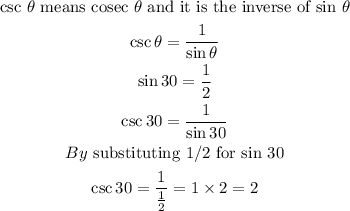
Therefore, the value of csc 30 is 2

STEP 3: Get the value of cot 60

`\begin{gathered} \cot \theta=(1)/(\tan \theta) \\ \tan 60=\sqrt[]{3} \\ \cot 60=\frac{1}{\sqrt[]{3}} \\ By\text{ rationalization,} \\ \frac{1}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}}=\frac{\sqrt[]{3}}{3} \end{gathered}`

Hence, the value of cot 60 is √3/3

STEP 4: Get the value of cos 30

`\begin{gathered} (\sin\theta)/(\tan\theta)=\cos \theta \\ \cos 30=(\sin 30)/(\tan 30) \\ By\text{ substitution,} \\ \cos 30=(1)/(2)/\frac{\sqrt[]{3}}{3} \\ \Rightarrow(1)/(2)*\frac{3}{\sqrt[]{3}}=\frac{3}{2\sqrt[]{3}} \\ By\text{ rationalization,} \\ \cos 30=\frac{3}{2\sqrt[]{3}}*\frac{2\sqrt[]{3}}{2\sqrt[]{3}}=\frac{3*2\sqrt[]{3}}{2*2*3}=\frac{6\sqrt[]{3}}{12}=\frac{\sqrt[]{3}}{2} \end{gathered}`

Hence, the value of cos 30 is √3/2

STEP 5: Get the value of cot 30

`\begin{gathered} \cot \theta=(1)/(\tan \theta) \\ \cot 30=(1)/(\tan 30) \\ By\text{ substitution,} \\ \cot 30=\frac{1}{\frac{\sqrt[]{3}}{3}} \\ \cot 30=1/\frac{\sqrt[]{3}}{3}=1*\frac{3}{\sqrt[]{3}}=\frac{3}{\sqrt[]{3}} \\ By\text{ rationalization,} \\ \frac{3}{\sqrt[]{3}}=\frac{3}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}}=\frac{3\sqrt[]{3}}{3}=\sqrt[]{3} \end{gathered}`

Hence, the value of cot 30 is √3