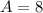Question

triangle GHI with vertices G(-4,2),H(-2,4), and I(-7,7) drawn in a rectangle. what is the area in square units of triangle GHI

Answer 1

Question:

Triangle GHI with vertices G(-4,2),H(-2,4), and I(-7,7) drawn in a rectangle. what is the area in square units of triangle GHI ​.

Solution.

By definition, the area of a triangle is:

`A\text{ = }\frac{b\text{ x h}}{2}`

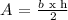
Now, the area of the triangle GHI is the area of the square minus the triangles that surround the triangle GHI.

The area of the square is:

Area of square =AS= b x h = 5 x 5 = 25

Area of left triangle =

`A_l\text{ = }\frac{b\text{ x h}}{2}\text{ = }\frac{3\text{ x }5}{2}=\text{ }(15)/(2)`

Area of the upper right triangle

`A_(sr)\text{ = }\frac{b\text{ x h}}{2}\text{ = }\frac{5\text{ x }3}{2}=\text{ }(15)/(2)`

Area of the lower right triangle

`A_(lr)\text{ = }\frac{b\text{ x h}}{2}\text{ = }\frac{2\text{ x }2}{2}=2`

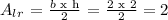
Thus, area A of the triangle GHI is:

`A=AS-(A_l+A_(sr)+A_(lr)\text{)}`

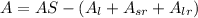
that is:

`A=25-(15+2_{}\text{) = 25-17 = 8}`

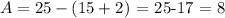
Then, we can conclude that the area of the triangle GHI is:

`A=\text{8}`