Question

Find the change in gravitational potential energy of each of the following a) A box of mass 10kg which is raised 1.6 meters vertically b)a lorry of mass 4000kg which travels 1600 meters up a plane, inclined at an angle of 15 degrees from the horizontal

Answer 1

`16,233.112\text{ }J`

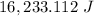
Step-by-step explanation

b) We want to find the change in gravitational potential energy of the lorry.

The change in gravitational potential energy is given by:

`\Delta PE=mg\Delta h`

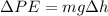
where m = mass of the lorry

g = acceleration due to gravity

Δh = change in height

Let us make a sketch of the problem:

To find the change in height, we have to apply the trigonometric ratios:

`\sin15=(\Delta h)/(1600)`

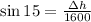
Therefore, the change in height is:

`\begin{gathered} \Delta h=1500*\sin15 \\ \\ \Delta h=414.11\text{ m} \end{gathered}`

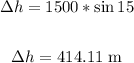
Therefore, the change in gravitational potential energy of the lorry is:

`\begin{gathered} \Delta PE=4000*9.8*414.11 \\ \\ \Delta PE=16,233.112J \end{gathered}`

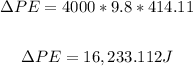
That is the answer.