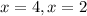Number 2:
To solve the quadratic equation by using the factorization method;
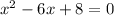
We note here that the factors of 8 that can also add up to -6 are -4 and -2.
Therefore we'll have;
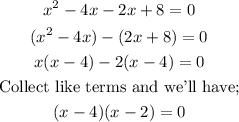
Therefore, we now have;
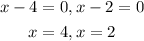
To solve the quadratic equation by using the quadratic equation formula, we would have;
![\begin{gathered} x^2-6x+8=0 \\ \text{The formula is;} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{Where;} \\ a=1,b=-6,c=8 \\ x=\frac{-\lbrack-6\rbrack\pm\sqrt[]{(-6^2)-4(1)(8)}}{2(1)} \\ x=\frac{6\pm\sqrt[]{36-32}}{2} \\ x=\frac{6\pm\sqrt[]{4}}{2} \\ x=(6\pm2)/(2) \\ \text{Hence, we now have;} \\ x=(6+2)/(2),x=(6-2)/(2) \\ x=(8)/(2),x=(4)/(2) \\ x=4,x=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u3kdkzieazj84nlwb9vz21w5u7ynx9gqz9.png)
Therefore, using the quadratic equation formula, we also have;