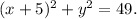Question

Write the standard form of the equation of the circle with its center at (- 5,0), and a radius of 7.

Answer 1

Given:

The centre of the circle, (h,k)=(-5,0).

The radius of the circle, r =7.

Required:

We need to find the standard form of the equation of the circle.

Step-by-step explanation:

Consider the standard form of the equation of the circle.

`(x-h)^2+(y-k)^2=r^2`

where (h,k) is the centre and r is the radius.

Substitute h =-5, k=0 and r =7 in the equation.

`(x-(-5))^2+(y-0)^2=7^2`
`Use\text{ \lparen-\rparen\lparen-\rparen=\lparen+\rparen and }7^2=49.`

`(x+5)^2+(y-0)^2=49`

`(x+5)^2+y^2=49`

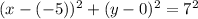
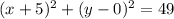
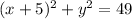
Final answer:

The standard form of the equation of the circle with its centre at (- 5,0), and a radius of 7 is

`(x+5)^2+y^2=49.`